
Physics
Let there be more light
The Dark Side of the Prism
Perhaps the second most famous graphic icon associated with Pink Floyd is the prism on the front cover of The Dark Side of the Moon. (I'll concede first place to the pig.) In a nice touch, the back cover shows a mirror image of the front cover (almost--the prisms are inverted compared to each other, but the colored light beam has the red beam on top on both sides) with the ray of white light crossing over from the back cover to the front to connect the covers into a single image.
 The Dark Side of the Moon |
The use of a prism to split white light into colors is a common phenomenon, but there is actually a lot of physics involved, some of which is counterintuitive. While "proper" physics involves numbers and equations, I'll keep the math to a minimum in the following explanation.
First off, what is a prism? The one illustrated on Dark Side of the Moon is the most common, called a right triangular prism. At this point, those of you who remember your high school geometry are probably screaming, "That's an equilateral triangle on the cover, not a right triangle." And you are correct. In reference to a prism, "right" refers to the prism as a whole, while "triangular" refers to the end. Think of it as a "triangular right prism," if that helps you separate the two concepts. Part of the confusion is that the side of the prism you see on the album cover is actually the "end." By definition, the ends of a prism are parallel and equal polygons. Three sides is the minimum that makes physical sense, but there can be more. Then there are the "faces" which connect the ends and are parallelograms equal in number to the sides of the ends. If the faces are perpendicular to the ends, it is a right prism. The traditional optical prism has triangular ends. If you place an end on the table, you will see that the faces are rectangles perpendicular to the ends. If the ends are not identical, the object is called a prismoid.
In optics, the term "prism" is almost always used to describe a triangular prism; i.e., where the ends are triangles, and an equilateral triangle is the most common end shape (as on the cover of Dark Side of the Moon), although other shapes are possible. In operation, the prism is placed face down, like a Van Halen fan at the end of a concert. With the prism placed on a face, the angle at the peak of the triangle is called the angle of dispersion.
Different angles of dispersion do lead to different effects, but the sixty-degree equilateral triangle is what's shown on the cover.
When a narrow beam of white light strikes a prism face at an angle, two phenomena occur: the beam is refracted (i.e. it changes direction and bends), and the beam is dispersed (i.e. the white light is broken into its constituent colors).
Refraction occurs when light passes from one medium into another. In the case illustrated on the cover, light is passing from air into glass (we can presume the prism is made of glass, although this is not always the case) and then from glass back into air again. Draw a line through the point where the light enters the first prism face such that the line is perpendicular to the prism face. (Err, you did realize I meant "an imaginary line," didn't you? Don't want you to mess up that collector's piece of a cover.) This line is called a "normal" to the surface. (Here "normal" means perpendicular. Yes, I realize your 'normal' posture is seldom completely perpendicular, but scientists tend to be rather rigid in their definitions.) The ray of light coming into the prism face is called the "incident ray," and the ray inside the prism is called the "refracted ray." The angle the incident ray makes with the normal is called the angle of incidence. (Not the angle between the face of the prism and the incident ray; it's the angle between the normal and the ray.) The angle between the normal and the refracted ray is the angle of refraction. Note that on the cover that the angle of incidence is larger than the angle of refraction (i.e. the light has been bent toward the normal).
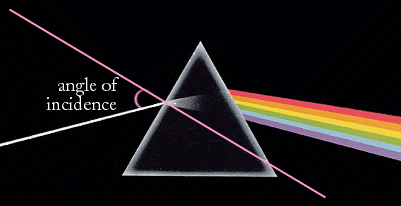 The pink line represents the 'normal', forming the angle of incidence with the incident (incoming) ray of light. |
The light is bending because of a change in "optical density" as the light passes from the air into the glass. In this case, the glass has a greater density than air, so the refracted ray is bent toward the normal. When the ray emerges from the glass into air, it is again refracted. But this time, because the optical density is going from greater to lesser, the ray is bent away from the normal. This is most clearly seen by looking at the back cover. And, yes, scientists do measure the optical density of substances such as air and glass. And they do it by comparing the angles of incidence and refraction, and the result is called the Index of Refraction.
If you were to change the angle of incidence, the angle of refraction would change as well. And in a very precise way. The Index of Refraction is equal to the sine of the angle of incidence divided by the sine of the angle of refraction. (Remember that these angles are measured between the rays and the normal to the surface.)
For those whose trigonometry skills have grown rusty from disuse, look at the angle of incidence between the incoming ray striking the prism and the normal to the prism's face. In this example, the incoming ray forms the left leg of the angle, and the normal forms the right leg. Go out along the normal to a convenient point and draw a line perpendicular to the normal that goes over to the incoming ray. You now have a right triangle (the angle between the normal and the line to the incoming ray is ninety degrees). The side of the triangle between the normal and the incoming ray is opposite to the angle of incidence, and the section of the incoming ray that is within the triangle is the hypotenuse of the triangle. The sine of the angle of incidence is the length of the opposite side divided by the length of the hypotenuse. Remember that I told you to pick any convenient point along the normal to the prism face to draw your perpendicular line to the incoming ray? What if you chose a different point? If you move the point further away from the prism face, the resulting right triangle will be larger. If you move the point in closer to the prism face, the right triangle will be smaller. The larger triangle will have a longer opposite side and a longer hypotenuse. The smaller triangle will have a shorter opposite side and a shorter hypotenuse. But in all cases, the ratio of the length of the opposite side to the length of the hypotenuse will be the same for a given angle.
Now we need to do the same thing with the angle of refraction inside the prism. The normal here is simply an extension of the normal in the air; it's still perpendicular to the prism face. Pick a point along the normal and draw a perpendicular line that reaches the refracted ray. Again we have a right triangle. The side between the normal and the refracted ray is opposite the angle of refraction, and the hypotenuse is the distance along the refracted ray between the face of the prism and where the perpendicular from the normal intersects the refracted ray. The sine of the angle of refraction is the length of the side opposite divided by the length of the hypotenuse.
Since the sines of the angles remain the same regardless of the size of the triangles, let's pick two triangles, one for the incident ray and one for the refracted ray, such that the length of the hypotenuse is the same for both triangles. In that case, the ratio of the sines (which is the Index of Refraction we're looking for) is equal to (the length of the side opposite the angle of incidence divided by the length of the hypotenuse) divided by (the length of the side opposite the angle of refraction divided by the length of the hypotenuse). Those of you who remember your fractions will recognize that the lengths of the hypotenuse divide out, and we are left with the Index of Refraction being equal to the length of the side opposite the angle of incidence divided by the length of the side opposite the angle of refraction. (Those who don't remember can "trust us", as Dave smirks in the Pompeii movie.) Because the angle of refraction was bent toward the normal, the length of its opposite side will be shorter than that of the side opposite the angle of incidence. With the smaller value on the bottom of the fraction, the Index of Refraction will be greater than one, which means the optical density of the refracting medium, in this case the prism, is greater than the optical density of the incident medium, air.
The definition of the Index of Refraction requires light to travel from one medium to another, and the value for a given interface between two media is really the ratio of the Index of each medium, so scientists need some basic value to compare everything with. The least optically dense material is a vacuum, so it was assigned the value one. If a vacuum has no optical density, why was it not assigned the value zero? Since we're dealing with ratios, we run into real problems if the denominator is zero. Defining it as one makes things much simpler.
Air has an Index of Refraction of 1.0002926, so unless you have access to really good equipment, the Index of Refraction for light passing from air into a substance will be close enough to the real value for government work. Water typically has an Index of 1.33. (The water from the Red Cedar River on Michigan State's campus has a much higher Index due to the duck droppings and other additives.) Glass can range from 1.4 to almost 2, depending on its composition and purity. Diamond is 2.4, and silicon is 4.01.
Can you have an Index of Refraction less than one? Well, that would require the side opposite the angle of refraction to be longer than the side opposite the angle of incidence, which would require the angle of refraction to bend away from the normal. This is exactly what happens when a beam of light emerges from the face of the prism into the air. This is more clearly seen on the back cover where the single beam of white light emerges, rather than on the front cover where the dispersion phenomenon dominates the view.
 |
Now the weird (read: interesting) thing is that the light is bending because the speed of light is changing at the interface. I can hear those of you who remember a little of your science classes sputtering, "But the speed of light is a constant! What about the slogan '186,000 miles per second. It's not only a good idea; it's the law.'?" Just like traffic speed limits, 186,000 miles per second is an upper limit. It happens to be the speed of light in a vacuum where there is nothing to slow the light down. But once light enters a physical medium, it slows down, even though the change is imperceptible to human senses. And if you review a history of the attempts to measure the speed of light, it's often imperceptible to highly sophisticated equipment as well.
Some science fiction authors have had fun with the concept. Bob Shaw came up with the idea of "slow glass" where it could take decades for the light to pass through the glass so that a window made of slow glass would be a window into the past because the light emerging from the window had entered it years ago. In Red Shift Rendevous, John Stith imagined a space station in which gravitational conditions slowed the speed of light down to where the human eye could detect its progress, and the old joke about "he was so fast, he could turn out the light and be under the covers before the room got dark" was literally true.
Of course, that's science fiction, and science fiction has nothing to do with Pink Floyd, right?
In the real world and on the cover of Dark Side of the Moon, the change in the speed of light causes the dispersion we see because the change in the speed of light is dependent on the wavelength of the light. When the light emerges from the prism, red is on top and blue/violet is on the bottom. The spread in colors follows the spread in wavelengths, with the blue beam spreading more widely than the red. This is not the case for all substances. There are substances, most commonly aniline dyes, that produce an inverted spectrum with the blue on top and the red underneath, but the spectra you are most likely to encounter, such as rainbows, will have the red on top. The mnemonic is "Blue bends best," and that is why the sky is blue, most of the time: the change from the vacuum of space into the atmosphere disperses the light, and the blue is spread out the most.
 Dark Side's back cover |
Now the back cover of the album shows a beam of colors entering a prism that is inverted compared to the prism on the front cover, and a beam of white light emerges. This is the artist's conceit and not really physically possible. If you were to take the inverted prism from the back cover, move it over to the front cover, and then place it just to the right of the front cover's prism, with the faces touching, the incident beam of white light would emerge from the second prism as white light again. There would most likely be some chromatic aberration; i.e., you would see some color blurring, but the emergent beam would be mostly white: the second, inverted prism would have negated the effect of the first prism. But that is with the two prisms touching so that the colors don't have time to spread out. The fiction on the back cover is that you could produce a beam of colors that would stay together like that over any significant distance. So, the back cover is a fiction, but it is a marvelous image.
What would happen if you were to send a beam from one of Pink Floyd's lasers through a prism? Well, the beam from a Pink Floyd laser would most likely completely engulf the prism so you wouldn't see any effect. So let's use a narrower beam, say from a laser pointer. When the light strikes the prism face, it will be refracted; i.e., it will bend, and because the prism is more optically dense than air, the beam will be bent toward the normal. As it emerges from the prism, it will be refracted again, this time bending away from the normal. But because a laser beam is monochromatic (i.e. one color), one wavelength, there will be no dispersion. Use a different colored laser, and you will get a slightly different angle of refraction for a given angle of incidence, but there will still be no dispersion. White light definitely produces a prettier picture.
Perhaps the third most famous graphic icon associated with Pink Floyd is the cow from the cover of Atom Heart Mother. Here's a quick anecdote about the physics of cows.
A farmer wanted to improve the operation of his dairy farm so he asked the scientists at the local university to submit proposals for what he should do. To his surprise, the physicist was the only scientist who guaranteed that his proposal would work. The farmer had his doubts, but, hey, a guarantee is a guarantee, so he gave the physicist the job. After three months of study, the physicist was ready to report his results. The physicist began by saying, "Assume a spherical cow..."
